On this page some basic physical principles are introduced:
Direct Current and Alternating Current:
Direct current is fixed with time, like the current that is drawn from a battery. So, direct current always flows in the same direction. Alternating current is different. It switches direction after a fixed period of time. The rate at which it reverses direction is it’s frequency. The mains power supply we receive in our homes is based on alternating current and is supplied at a frequency of 60Hz. This means that it changes direction 60 times every second. These concepts are illustrated below:
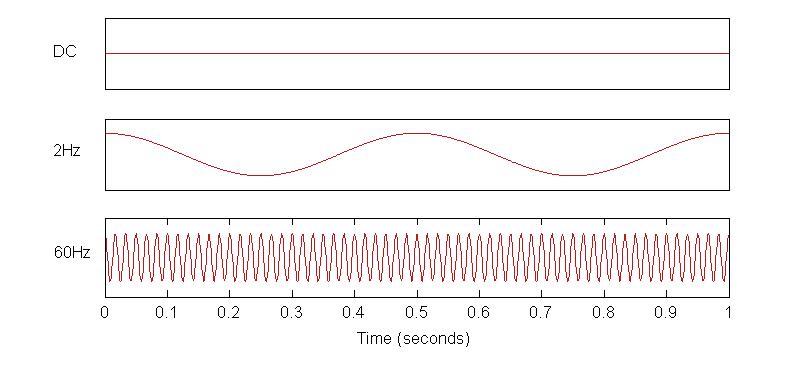
The frequency of the current dictates how many cycles or direction reversals there are in a second
The uppermost trace depicts direct current so it has a fixed value and is constant with time. The middle trace depicts alternating current with a frequency of 2Hz. This means that it completes two full cycles in a second (the time span of the trace). The bottom trace depicts alternating current with a frequency of 60Hz so now the pattern is repeated sixty times across the trace. This might seem like a lot but when we do impedance analysis we often look at much higher frequencies, for example up to 10MHz. This means 10,000,000 cycles in just one second! This illustrates that frequency is inversely proportional to time. In other words, a lower frequency takes a longer time to trace out. From the traces above it can be seen that for the 2Hz signal it takes half a second (1/2 seconds) to map out one cycle whereas for the 60Hz cycle it only takes sixteen thousands of a second (1/60 seconds). This is important to bear in mind for the discussion about reactance below.
Resistance & Reactance:
Resistance is defined as the capacity to oppose. So, in electrical terms resistance is a measure of the capacity of an object to oppose the flow of current. To put it another way, it is a measure of how much charge can be transferred through an object in one second. This quantity is measured in Ohms (Ω), named after the German physicist Georg Ohm. Since resistance is a measure of the charge transfer per unit time, it is will remain the same regardless of the frequency of the current.
Reactance is similar to resistance in that it describes the opposition to current flow but it specifically refers to charge storage rather than charge transfer. Storing anything takes time and so the reactance depends on how long it has to store charge or, equivalently, it depends on the frequency of the alternating current (since, as shown above, frequency is inversely proportional to time). The lower the frequency the longer there is to store charge and therefore restrict current flow (since these charges can’t now contribute to direct current flow). An object that exhibits reactance rather than resistance is one that has an ability to store rather than simply transfer energy.
Bioimpedance:
We can put these concepts together to examine the behaviour of biological samples. Tissue can be split up into three main compartments: the cell membranes separate the tissue into the extracellular space and the intracellular space. The intracellular and extracellular spaces contain various ionic species, e.g. proteins, sodium ions and calcium ions. The presence of these charge carriers mean that these spaces act as resistors. The cell membranes are different. Charges cannot simply flow through these boundaries. Instead they build up. This charge build-up (or charge storage) means that the electrical behaviour of the cell membranes can be represented by a capacitive reactance.
Impedance quantifies an object’s complete capacity to oppose the flow of current including both it’s reactance and it’s resistance. Tissue has an impedance since it is a combination of the resistive intra- and extracellular components as well as the charge storing nature of the cell membranes. The term bioimpedance specifically refers to the electrical impedance of biological samples be it tissue, cell cultures, whole body, etc.
To investigate the behaviour of a tissue it is helpful to create a model of it’s electrical behaviour. We can do this by using electronic components to represent each of the compartments discussed above. This means that in the simplest case we have three components: two resistors (one each for the extra- and intracellular spaces) and a capacitor (for the cell membrane). To configure these components in an equivalent electrical circuit, we have to consider how the current flows through the tissue. There are two options. Either current can flow outside the cells or inside the cells. In electrical circuit, options are represented as parallel paths (one path for each option). If the current flows through the intracellular path then it will not only have to pass through the intracellular resistance but also through the cell membrane. For this reason the model that results is as shown below:
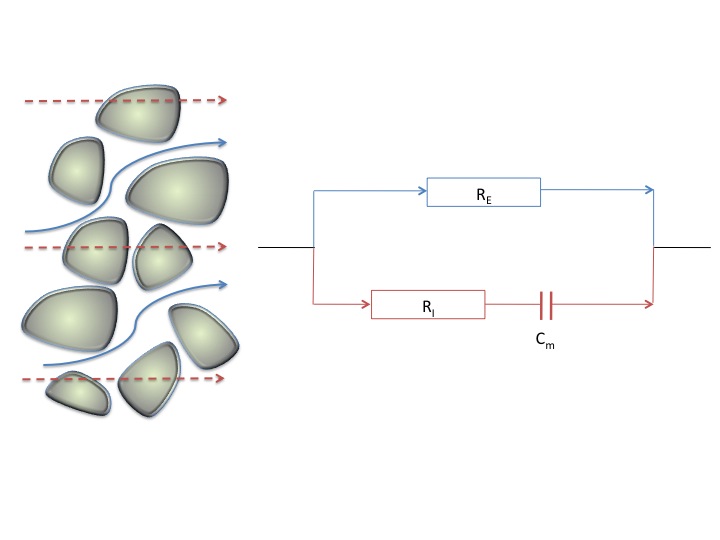
The Cole model puts forward two routes for current flow: intracellular and extracellular. The extracellular route is a pure resistance whereas the intracellular route has a resistance and a reactance associated with it.
Here RE is the extracellular resistance – a measure of the resistance to current flow in the spaces outside the cells; RI is the intracellular resistance – a measure of the resistance to current flow within the cells – and Cm is the membrane capacitance – a measure of how much charge accumulates at the boundary of the cell. The route through the cells only becomes viable at high frequency. At low frequency the cell membrane blocks the current flow because all of the charges accumulate at the interface. At higher frequency the direction of current flow changes very quickly and so charges no longer build up and the membrane no longer limits the amount of charge that flows.
This equivalent circuit model of the electrical behaviour of cells is referred to as “The Cole Model” after the Cole brothers who first proposed it. The values the components have is dependent on the composition of the tissue. It is this dependence that gives us the opportunity to distinguish between different tissue types based on their electrical parameters.
The impedance profile that results from such a model is discussed in greater detail here
